Creating a stock market simulation

Mathematics

By Oscar Kelk • 9 minutes to read

Created 18 June, 2023 at 11:00 PM

Supply and demand are the two factors which influence share prices within a stock market. When people buy, it rises. When people sell, it falls.

Some weeks ago I began a stock market simulation on a website run by myself and a friend. We already had a money system so I could implement it simply, the prospect being that players would deposit and withdraw cash, having it multiply daily.

And so this is how it continued for 3 days. Player accounts had 2 data fields: cash, and money (in shares). Every day you loaded the page - and if your money (in shares) hadn't yet been updated, a randomly generated multiplier seeded by the day's unix timestamp (12 am) was applied.

This seemed fine, but this system ended up going under heavy revision.

SM Stocks: Phase 2

Having the value of your shares wasn't realistic, and didn't allow for thorough manipulation, so first I changed the way the data was handled - each account now had a shares field in place of the money (in shares) field. In this new handling you would be told both how many shares you had, and what they worth - based on the share price. And the share price was what was changed.

Now every day the share price would be randomly multiplied; it could be anywhere from halved to doubled. But this didn't last.

SM Stocks: Phase 3

Allow me to introduce someone: I doubt he'd want to be named, so we'll give him a pseudonym: "Walter". Walter is a very strong fan of the website, and as you'll see he made quite a contribution to the system.

Walter was concerned with the lack of that principle I outlined earlier; whether someone bought at a low price or sold at a low price, they were equally as likely to make or lose money.

I first trialled a system in which the share price would be randomly added to or subtracted from. After running a simulation I saw that this would have created wild peaks and troughs in the share price (see below) which would sometimes run into a complete crash. Furthermore, it didn't really solve Walter's problem, so this too was only shortly in place.

Share price graph extremely peaking at the beginning before slowly falling into a crash

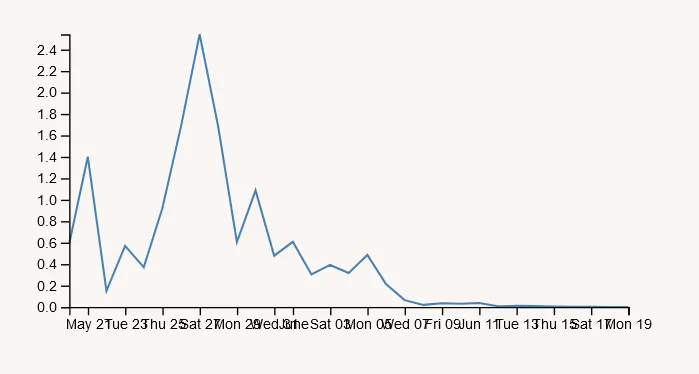
30 day simulation of the system

SM Stocks: Phase 4 - The formulas

Warning: maths

Walter and I spent more than an hour just figuring out a viable formula for the share price. Criteria was as follows:

Must be influenced by transactions (and live - not only daily!)
Must not be cheatable in any sense

But this is easier said than done! Imagine the new share price is simply calculated as the product of the old share price and the shares bought.

p r i c e_{n e w} = p r i c e_{o l d} \times s h a r e s_{b o u g h t}

p r i c e_{n e w} = \frac{p r i c e_{o l d}}{s h a r e s_{s o l d}}

Take this hypothetical player: Gobi. Gobi has $200,000 in his account, and at the moment the share price is $1, so he decides to buy.

Now Gobi has 200,000 shares, and the price is $200,000. See the problem?

Cash	Shares	Share price
$200,000	0	$1
$0	200,000	$200,000
$40,000,000,000	0	$1

Great. Now Gobi has made almost 40 billion dollars by doing absolutely nothing. And if he likes he may do it again, and again, and again.

How might this be solved? We tried modelling it after the real world. What if there was a certain amount of money owned by the 'company' which was split out among the total amount of shares?

p r i c e_{n e w} = \frac{m o n e y_{t o t a l}}{s h a r e s_{t o t a l}}

Then we simulated, where Gobi (who still has $200,000) invests in the company, which begins with $20,000 and 5 shares.

Gobi's cash	Gobi's shares	Company funds	Shares left	Share price
$200,000	0	$20,000	5	$4,000
$196,000	1	$24,000	4	$6,000
$190,000	2	$30,000	3	$10,000
$180,000	3	$40,000	2	$20,000
$160,000	4	$60,000	1	$60,000

Once again. Gobi has 4 shares, each worth $60,000. From here he sells them for a total of $240,000, doubling his initial balance. So where is all this money coming from? The problem lies in the fact that each share is being bought at a lower price than what they are being sold for. In our simulation the first share was bought for $56,000 less than it was sold for. How can that be right?

Here's what we did: the shares, instead of being bought for the share price, are bought for what the share price will be after the shares are bought.

So when buying this is used:

p r i c e_{n e w} = p r i c e_{o l d} + m u l t i p l i e r \times s h a r e s \times p r i c e_{o l d}

And for selling, its inverse:

p r i c e_{n e w} = \frac{p r i c e_{o l d}}{m u l t i p l i e r \times s h a r e s + 1}

Note the multiplier. This is in place to tone down the price a little bit - keep it at a reasonable level (if someone bought 200,000 shares, we wouldn't want the price at $200,000!).

Here I thought finally we had it. I wrote the code and was ready to push it to the website. Then, Walter came to me with a glaring concern. People could still make money by buying shares individually (as opposed to the whole lot at once). He came to me with his solution, newly written formulas which ensured each share was considered individually no matter how many are purchased.

When buying shares

p r i c e_{n e w} = p r i c e_{o l d} \times (m u l t i p l i e r + 1)^{s h a r e s}

i n v e s t m e n t = \frac{p r i c e_{o l d} \times ((m u l t i p l i e r + 1)^{s h a r e s} - 1) \times (m u l t i p l i e r + 1)}{m u l t i p l i e r}

The investment formula is how much one would need to pay, based on how many shares they want to buy. It's a geometric sequence :)

Another feature of the simulation is the "money's worth" option. Instead of inputting how many shares they wish to buy, players may input how much money they wish to invest. For the calculation of shares from money, we use the following (rearranged from above):

s h a r e s = \frac{\ln (\frac{m u l t i p l i e r \times i n v e s t m e n t + p r i c e_{o l d} \times (m u l t i p l i e r + 1)}{p r i c e_{o l d} \times (m u l t i p l i e r + 1)})}{\ln (m u l t i p l i e r + 1)}

When selling shares

p r i c e_{n e w} = \frac{p r i c e_{o l d}}{(m u l t i p l i e r + 1)^{s h a r e s}}

i n v e s t m e n t_{r e t u r n} = \frac{p r i c e_{o l d} \times (m u l t i p l i e r + 1) (1 - {(\frac{1}{m u l t i p l i e r + 1})}^{s h a r e s})}{m u l t i p l i e r}

And of course rearranged:

s h a r e s = \frac{\ln (\frac{- (m u l t i p l i e r \times i n v e s t m e n t_{r e t u r n} - p r i c e_{o l d} \times (m u l t i p l i e r + 1))}{p r i c e_{o l d} \times (m u l t i p l i e r + 1)})}{\ln (\frac{1}{m u l t i p l i e r + 1})}

Conclusion

So now I'm just letting it run. I'll see how it ends up in a few weeks and whether there are any tweaks that need to be made. I have identified some issues with graph rendering and the like, and I know how to fix them, but they're so minor that I'd rather just let them be.

If you are thinking of making a stock market game and you don't know how to calculate share price - it really should be based off purchases and sales of shares. Don't bother with any randomness unless you can find a better way to make it work!

Formulas

Here are the currently in-use formulas, in a more readable form.

Where:

a = amount to pay or paid back
n = number of shares bought or sold
p = share price
c = multiplier constant (currently set to 1/50000)

When buying:

p_{n e w} = p_{o l d} (c + 1)^{n}

a = \frac{p_{o l d} ((c + 1)^{n} - 1) (c + 1)}{c}

n = \frac{\ln (\frac{c a + p_{o l d} (c + 1)}{p_{o l d} (c + 1)})}{\ln (c + 1)}

When selling:

p_{n e w} = \frac{p_{o l d}}{(c + 1)^{n}}

a_{r e t u r n} = \frac{p_{o l d} (c + 1) (1 - {(\frac{1}{c + 1})}^{n})}{c}

n = \frac{\ln (\frac{- (c a_{r e t u r n} - p_{o l d} (c + 1))}{p_{o l d} (c + 1)})}{\ln (\frac{1}{c + 1})}

Viewed 5943 times

arrow_upward